Introduction to Fractions
Explore Fractions with this Interactive Lesson
Click on any fraction or create your own to see how it looks as a part of the whole circle!
Create Your Own Fraction
/Quiz Time!
What are Fractions?
Fractions are used to indicate the number of parts of a whole. Suppose you go to Domino's pizza and order a medium pizza. If your pizza has 8 slices and you did not eat the whole pizza, this means that parts of the whole pizza will be left on the pizza box.
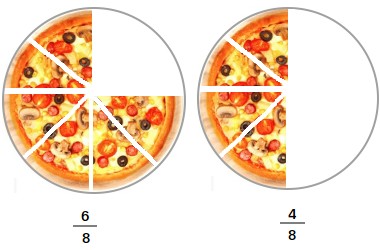
The pizza on the left shows six-eighths (6/8) and the pizza on the right shows four-eighths (4/8).
6/8 and 4/8 are called fractions.
The top number is the numerator of the fraction and it tells us how many slices there are.
The bottom number is the denominator of the fraction and it tells us how many equal slices there are in total.
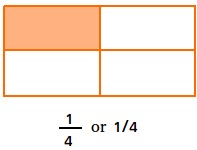
Notice that a forward slash (/) or a horizontal line may be used to separate the numerator from the denominator. Because the horizontal line is more appealing, we prefer to use it instead of a forward slash.
Equivalent fractions
Now, take a look at the figure below. You can clearly see that six-eighths (6/8) of a whole pizza is the same as three-fourths (3/4) of a whole pizza.
6/8 and 3/4 are equivalent fractions. Although 6/8 and 3/4 have different numerators and different denominators, they are both equal.
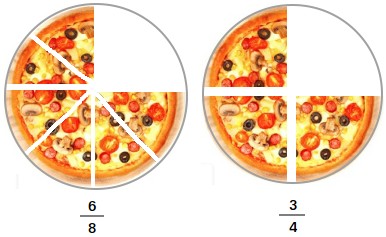
In fact, 6/8 = 3/4 = 0.75
More examples of equivalent fractions
Higher terms and lower terms of fractions
Notice that to get from 1/2 to 4/8, all we need to do is to multiply both the numerator and the denominator of 1/2 by the same number or 4.
In the same way, to get from 1/3 to 5/15, we can multiply both the numerator and the denominator of 1/3 by 5.
4/8 and 5/15 are called higher terms of 1/2 and 1/3 respectively.
Be careful! 4/8 is not bigger than 1/2 and 5/15 is not bigger than 1/3.
4/8 is a higher term of 1/2 only because it has a bigger numerator and a bigger denominator. However, we saw before that 1/2 and 4/8 are equivalent fractions since 1/2 = 4/8 = 0.5
Notice too that you can go from a higher term to a lower term. For instance, to bring 5/15 to a lower term, all you need to do is to divide both numerator and denominator by 5. You will get 1/3.
Simplifying a fraction is the process of going from higher terms to lower terms. To get the simplest form of a fraction, divide the numerator and the denominator by the greatest common factor (gcf) or the largest number that divides into both numerator and denominator evenly.
For instance, to bring 10/40 to its simplest from, divide both 10 and 40 by 10. You will get 1/4.
1/2 and 1/3 are the lowest terms of 4/8 and 5/15 respectively.
Adding fractions
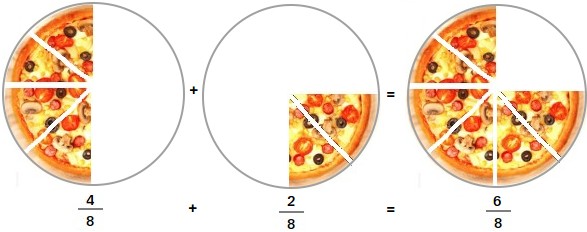
When the fractions have a common denominator (same denominator), add the numerators and keep the same denominator.
4/8 + 2/8 = (4 + 2)/8 = 6/8
Notice that 1/2 = 4/8 and 1/4 = 2/8. Therefore, 1/2 + 1/4 = 4/8 + 2/8 = 6/8.
If the denominators are not the same, you will need to look for the least common multiple (LCM) of the denominators. See adding fractions for more explanations.
Using fractions to show ratios
You can use a fraction to show a ratio. In a ratio, the numerator shows the part of a group you are considering and the denominator show the rest of the group or the whole group.
Suppose a class has 6 boys and 10 girls. What is the ratio of boys to girls. In this example, the numerator is the number of boys and the denominator is the rest of the group or the number of girls.
What is the ratio of girls to the total number of students? In this case, the numerator is the number of girls and the denominator is the whole group or the total number of students.
Using fractions to show division
A fraction can also be used to represent division.
You can then write the fraction as a decimal. For example, 4/5 = 4 ÷ 5 = 80/100 = 0.8
Benchmark fractions
Benchmark fractions are fractions that are used a lot in basic math and they are also helpful in picturing other fractions.
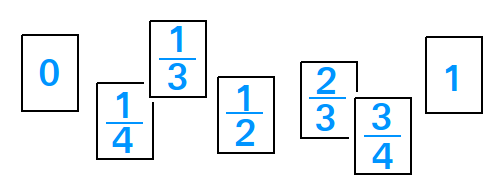
With benchmark fractions, you can do the followings:
- Quickly compare and order fractions. For example, 2/3 is bigger than 1/4.
- Round fractions and mixed numbers. For example, 3/4 rounds up to 1 since it is closer to 1 than to 0.
- Estimate sums and differences of fractions and mixed numbers. For example, 3/4 + 1/3 is bigger than 1 since 1/3 is bigger than 1/4.
A couple of examples showing how fractions are used in everyday life
1. If you cook a lot by following a recipe, then you must have used fractions a lot before.
Suppose a recipe says to use 12 tablespoons of sugar to make a cake weighing 3 pounds. How much sugar will you use for a one-pound cake?
Since you are making 1/3 of the whole cake, you may reason that you need to use 1/3 of 12 tablespoons.
2. Nurses and pharmacists must absolutely be good at fractions in order to give patient the correct dosage of a medication. Suppose the dosage strength of a medication is 100 mg. If the doctor orders 25 mg, how many tablets will you give? Nurses and pharmacists may need the following formula to solve this problem,
Nurses and pharmacists must know that 25/100 and 1/4 are equivalent fractions so they can give 1/4 of the tablet to the patient.