Parallelogram
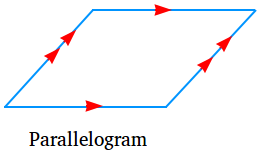
A parallelogram is a special quadrilateral with both pairs of opposite sides parallel as shown in the figure below. Notice that the opposite sides that are parallel lines are shown using the same amount of arrow heads.
Types of parallelogram
Squares, rectangles, and rhombuses are also parallelograms, more specifically special parallelograms, since their opposite sides are parallel according to the definition.
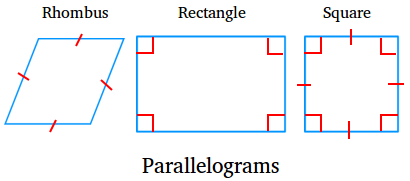
A rhombus is a parallelogram with four equal sides.
A rectangle is a parallelogram with four right angles
A square is a parallelogram with four equal sides and four right angles. Therefore, a square is a rhombus and a rectangle at the same time.
Diagonal, base, altitude, and height of a parallelogram
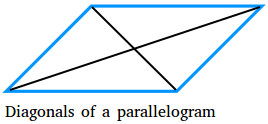
The diagonal of a parallelogram is a line segment that joins two vertices that are not next to each other. A parallelogram has two diagonals. The diagonals are shown in black in the figure below.
A base of a parallelogram is any of its sides.
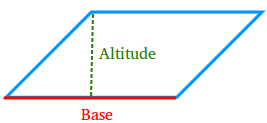
The altitude of a parallelogram is a line segment that starts from a vertex and is either perpendicular to the base or to the line containing the base.
In the figure above, the altitude is perpendicular to the base. However, in the figure below, the altitude is perpendicular to the line containing the base.
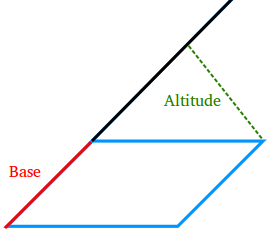
The height of a parallelogram is the length of an altitude.
Properties of parallelogram
- Opposite sides of a parallelogram are congruent.
- Opposite angles of a parallelogram are congruent.
- The diagonals of a parallelogram bisect each other.
- Consecutive angles are supplementary or add up to 180 degrees.
- Each diagonal of a parallelogram turns the parallelogram into 2 congruent triangles.
Please check the lesson about properties of a parallelogram to learn more about these 5 properties of parallelograms.
How to construct a parallelogram using a straightedge and compass
You can easily construct a parallelogram by following carefully the following 4 straightforward steps.
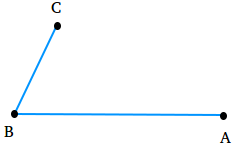
Step 1
Draw an angle ABC of any measure
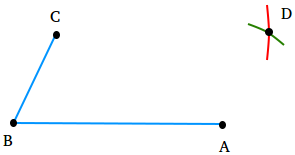
Step 2
Put the needle of a compass at point B and adjust the opening of the compass to measure the length of segment BA. Then, keeping the opening of the compass the same, put the needle of the compass at point C and draw an arc.

Step 3
Put the needle of a compass at point B and adjust the opening of the compass to measure the length of segment BC. Then, keeping the opening of the compass the same, put the needle of the compass at point A and draw an arc.
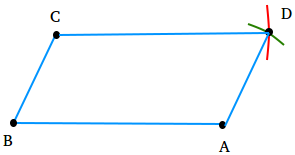
Step 4
Label the point of intersection of the two arcs D. Then, draw line segments AD and CD.
Perimeter of a parallelogram
Suppose you have a parallelogram ABCD. The perimeter is equal to the sum of the lengths of its sides.
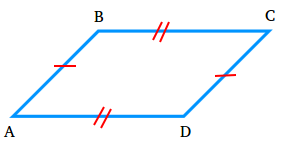
The length of segment AB is equal to the length of segment CD.
The length of segment BC is equal to the length of segment AD.
Perimeter = length of segment AB + length of segment AB + length of segment BC + length of segment BC
Perimeter = 2(length of segment AB) + 2(length of segment BC)
Area of a parallelogram

The area of a parallelogram is the product of the base and the length of the altitude.
Let h be the length of the altitude or the height of the parallelogram.
Then, the formula to use to find the area of a parallelogram is area = b × h
Notice that the term base refers both to the length of the base and the segment.
Parallelogram FAQs
-
It depends on which definition is used for a trapezoid! Parallelograms must have two pairs of opposite sides that are parallel. Some textbooks say that trapezoids must have exactly one pair of parallel sides. If there is exactly one pair of parallel sides, then the answer is no. Other textbooks say that trapezoids must have at least one pair of parallel sides. In this case, all parallelograms are trapezoids since they fit inside the definition of trapezoids.
-
It depends on which definition is used for a trapezoid! Parallelograms must have two pairs of opposite sides that are parallel. Some textbooks say that trapezoids must have exactly one pair of parallel sides. If there is exactly one pair of parallel sides, then the answer is no. Other textbooks say that trapezoids must have at least one pair of parallel sides. In this case, some trapezoids could become parallelograms if these trapezoids have two pairs of opposite sides that are parallel.
-
Yes! If you add up the 4 angles in any parallelogram, it will equal to 360 degrees.
-
No! A parallelogram will end up having 4 right angles if just one of the angles is a right angle. In this case, it is called a rectangle.
-
A quadrilateral is a polygon with 4 sides. Since every parallelogram has 4 sides, every parallelogram is also a quadrilateral.
-
In the American term, a trapezium is a quadrilateral that has no parallel sides. It is kind of the "opposite" of a parallelogram which has two pairs of parallel sides.