Properties of a parallelogram

The properties of a parallelogram are listed below. We will use a parallelogram ABCD to show these properties.

Property #1

Opposite sides of a parallelogram are congruent.

The length of AB is equal to the length of DC.
The length of BC is equal to the length of AD.

Here is how to prove that opposite sides of a parallelogram are congruent.

Property #2

Opposite angles of a parallelogram are congruent.

Angle A is equal to angle C
Angle B is equal to angle D

How to prove that the opposite angles of a parallelogram are congruent angles

Given parallelogram ABCD, we need to prove ∠A ≅ ∠C; ∠B ≅ ∠D

1. Given

ABCD is a parallelogram

2. Consecutive angles are supplementary angles in a parallelogram (property #4)

∠A + ∠B = 180 degrees 

∠B + ∠C = 180 degrees 

3. Transitive property in properties of equality

∠A + ∠B = ∠B + ∠C

4. Subtraction property in properties of equality

∠A + ∠B - ∠B = ∠B - ∠B + ∠C

5. ∠A  =  ∠C

Using similar reasoning, you can show that ∠B ≅ ∠D

Property #3

The diagonals of a parallelogram bisect each other.

Diagonal AC (red line) intersects and bisects diagonal BD (green line) at E.

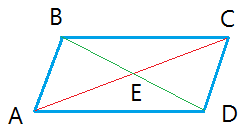
How to prove that the diagonals of a parallelogram bisect each other

Given parallelogram ABCD, we need to prove that segment AC and segment BD bisect each other at E.

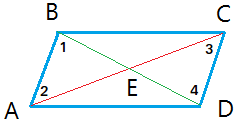
1. Given

ABCD is a parallelogram

2. Definition of parallelogram

Segment AB || segment DC

3. Parallel lines cut by a transversal form congruent alternate interior angles

∠1 ≅ ∠4; ∠2 ≅ ∠3

4. Opposite sides of a parallelogram are congruent

Segment AB ≅ segment DC

5. Triangle ABE is congruent to triangle CDE by ASA (angle-side-angle)

6. Segment AE ≅ segment CE and segment BE ≅ segment DE by CPCTC (corresponding parts of congruent triangles are congruent)

7. Definition of bisector

Segment AC and segment BD bisect each other at E.

Property #4

Consecutive angles are supplementary or add up to 180 degrees.

Angle A + angle B = 180 degrees
Angle B + angle C = 180 degrees
Angle C + angle D = 180 degrees
Angle D + angle A = 180 degrees

Property #5

Each diagonal of a parallelogram turns the parallelogram into 2 congruent triangles.

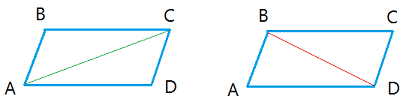
Triangle ABC is congruent or identical to triangle ADC.
Triangle BCD is congruent or identical to triangle BAD.

Using the properties of a parallelogram to solve math problems

Example  #1: Use the parallelogram below to find the length of segment BC and segment AD.

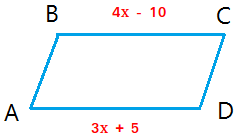
Since the opposite sides of a parallelogram are congruent, the length of segment BC is equal to the length of segment AD.

4x - 10 = 3x + 5.

Subtract 3x from each side

4x - 3x - 10 = 3x - 3x + 5

Simplify each side

x - 10 = 5

Add 10 to both sides of the equation.

x - 10 + 10 = 5 + 10

Simplify

x = 15

BC = AD = 4x - 10 = 4 times 15 - 10 = 60 - 10 = 50

Example  #2: Use the parallelogram below to find the length of segment AC and segment BD.

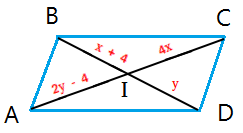
Since the diagonals of a parallelogram bisect each other, we get the following results:

• The length of segment AI is equal to the length of segment CI 

• The length of segment BI is equal to the length of segment DI 

This leads to a system of linear equations to solve

2y - 4 = 4x  

y = x + 4

Substitute x + 4 for y in 2y - 4 = 4x

2(x + 4) - 4 = 4x

Distribute

2x + 8 - 4 = 4x

Simplify

2x + 4 = 4x

Subtract 2x from each side

2x - 2x + 4 = 4x - 2x

Simplify

4 = 2x

x = 4/2 = 2

y = x + 4 = 2 + 4 = 6

AC = AI + CI = 2y - 4 + 4x = 2×6 - 4 + 4×2 = 12 - 4 + 8 = 16 

BD = BI + DI = x + 4 + y = 2 + 4 + 6 = 12 

Check also the lesson about parallelogram to learn some interesting stuff about the parallelogram such as:

• What is a parallelogram?
• Types of parallelogram such as rhombus and rectangles
• Perimeter of a parallelogram
• Area of a parallelogram