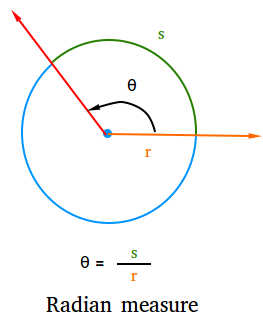
Definition of radian measure
The radian measure of any central angle is the length of the intercepted arc divided by the length of the radius of the circle.
In other words, it is the ratio of the arc length to the length of the radius of the circle.
In the figure below, notice that the central angle of the circle intercepts an arc whose length is twice the length of the radius of the circle.
The radian measure of the angle θ = length of the intercepted arc / length of radius
θ = 2r / r = 2. Thus, angle θ measures 2 radians or simply 2 rad.
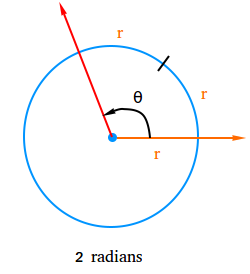
By the same token, the measure of a central angle that intercepts an arc whose length is equal to the length of the radius of the circle is 1 radian since r / r = 1.
How to find the radian measure of any angle when the arc length and the radius of the circle are given
In general, consider an arc whose length is s on a circle of radius r. The radian measure of the central angle, θ , that intercepts the arc is θ = (s / r) radians.
If the angle θ makes a full rotation, then the length of the arc is the circumference of the circle.
The formula to use to find the circumference of a circle is 2pir.
s = 2pir
θ = (2pir / r) radians.
θ = 2pi radians or 2π radians with pi = π = 3.14
A few examples showing how to find the radian measure
Example #1:
A circle has a radius equal to 4 inches. If a central angle, θ , intercepts an arc of length 20 inches, what is the radian measure of the central angle θ ?
θ = s / r = 20 inches / 4 inches = 5
Example #2:
A circle has a radius equal to 9 centimeters. If a central angle, θ , intercepts an arc of length 36 centimeters, what is the radian measure of the central angle θ ?
θ = s / r = 36 centimeters / 9 centimeters = 4
Notice that the units used in the problems above are inches and centimeters and they were canceled when we use the formula for radian measure. Now, we are left with a number that does not have a unit. Therefore, if an angle has a measure of 5 radians, we can write θ = 5 radians or simply 5. If the angle is measured in degree, then we must use the degree symbol. If the degree symbol is not used, then we can assume that the angle is measured in radians.
Example #3:
A youngster sitting on a merry-go-round moves clockwise through an arc length of 2.355 meters. If the youngster’s angular displacement is 1.57 rad, how far is the youngster sitting from the center of the merry-go-round?
What we are looking for is the radius of the merry-go-round.
Using the formula θ = s / r, we know that r = s / θ
r = 2.355 / 1.57
r = 1.5 m
Since the radius of the merry-go-round is 1.5 m, the distance the youngster is sitting from the center is 1.5 m
Just like degrees, radians measure the amount of rotation from the initial side to the terminal side of an angle.
For example, 1 radian is equal to 57.297 degrees, so the amount of rotation for the central angle from the initial side to the terminal side is 57.297 degrees.
Radian measure FAQs
-
1 radian in terms of pi is equal to 180/pi. Read carefully the lesson about converting degrees to radians to see why.
-
1 radian in radians is equal to 1 radian, 1 rad or just 1 without writing the unit. This usually happens when the central angle intercepts an arc that has the same length as the radius of the circle.
-
As stated in this lesson, 2π radians is a full rotation around a circle and this is equal to 360 degrees. Therefore, you can use the equation 2π radians = 360 degrees to find the measure of an angle in radians.
-
2π radians = 360 degrees
Divide both sides by 2π
Radian = 360/2π
Radian = 360/2(3.1415)
Radian = 360/2(6.283)
Radian = 57.29
Therefore, 1 radian is equal to 57.297 degrees