Sum of Arithmetic Series
Before I show you how to find the sum of arithmetic series, you need to know what an arithmetic series is or how to recognize it.A series is an expression for the sum of the terms of a sequence.
For example, 6 + 9 + 12 + 15 + 18 is a series for it is the expression for the sum of the terms of the sequence 6, 9, 12, 15, 18.
By the same token, 1 + 2 + 3 + .....100 is a series for it is an expression for the sum of the terms of the sequence 1, 2, 3, ......100.
To find the sum of arithmetic series, we can start with an activity.
The arithmetic series formula will make sense if you understand this activity. Focus then a lot on this activity!
Sum of Arithmetic Series: How to find the sum of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Using the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Add the first and last terms of the sequence and write down the answer.
Then, add the second and next-to-last terms.
Continue with the pattern until there is nothing to add.
We get:
1 + 10 = 11
2 + 9 = 11
3 + 8 = 11
4 + 7 = 11
5 + 6 = 11
What patterns do see? The sum is always 11.
11 + 11 + 11 + 11 + 11 = 5 × 11 = 55
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
As you can see instead of adding all the terms in the sequence, you can just do 5 × 11 since you will get the same answer.
Notice also that 5 × 11 =
10
2
× 11
Sum =
10
2
× (1 + 10)
We can make a generalization that will help us find the sum of arithmetic series.
Notice that 1 is the first term of the sequence. Notice also that 10 is the last term of the sequence.
Sum =
10
2
× (first term + last term)
For
10
2
,
10 is the number of terms in the sequence since the sequence has 10 terms.
Sum of Arithmetic Series Formula

Sum =
number of terms
2
× (first term + last term)
The following notation is more commonly used to find the sum of arithmetic series.
The sum Sn of a1 + a2 + a3 + a4 + ... + an is Sn =
n
2
× (a1 + an )
n is the number of term, a1 is the first term, and an is the nth or last term.
You will have no problem now to find the sum of 1 + 2 + 3 + 4 + ... + 100.
n = 100, a1 = 1, an = 100
Sn =
100
2
× (1 + 100 )
Sn = 50 × 101 = 5050
Find the sum of the arithmetic series 5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 + 50
n = 10, a1 = 5, an = 50
Sn =
10
2
× ( 5 + 50 )
Sn = 5 × 55 = 275
Observation:
5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 + 50 = 5 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10)
We already found the sum of 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 above. It is 55.
5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 + 50 = 5 × 55 = 275
How to Find the Number of Terms or n when Looking the Sum of Arithmetic Series
When looking for the sum of arithmetic series, it is not always easy to know the number of terms or n.
Just use the formula below to find n.
last term - first term
common difference
+ 1
The common difference is the same number that is added to each term
How many term here? 2 + 6 + 10 + 14 + ... + 78
Common difference is 4
Number of terms =
78 - 2
4
+ 1 = 19 + 1 = 20 terms
Summation Notation:
See the summation notation for the series 8 + 14 + 20 + 26 + 32 + 38. If you are having hard time to derive the explicit formula, review arithmetic sequence. The technique is explained in arithmetic sequence.
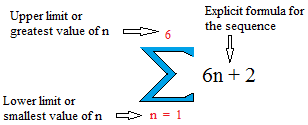
As you can see when
n = 1, 6 ×1 + 2 = 6 + 2 = 8
n = 2, 6 ×2 + 2 = 12 + 2 = 14
n = 3, 6 ×3 + 2 = 18 + 2 = 20
n = 4, 6 ×4 + 2 = 24 + 2 = 26
n = 5, 6 ×5 + 2 = 30 + 2 = 32
n = 6, 6 ×6 + 2 = 36 + 2 = 38
The big Greek letter that looks like an E is the Greek capital letter sigma. It is the equivalent of the English letter S for summation.
Find the summation notation for 5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 + 50
A good observation may help you see that 5n is the explicit formula for 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
Why? when n = 1, 5 × 1 = 5, when n = 2, 5 × 2 = 10, and so forth...
The upper limit is 10 since we have 10 terms
The lower limit is 1
$$ S_n = \sum_{i=1}^{10} 5n $$