Simple vs compound interest

Simple vs compound interest is not hard to understand. Basically, simple interest is interest paid on the original principal only while compound interest is interest paid not only on the principal, but also on the interest previously earned. The formulas that show the difference between simple interest and compound interest are shown below.

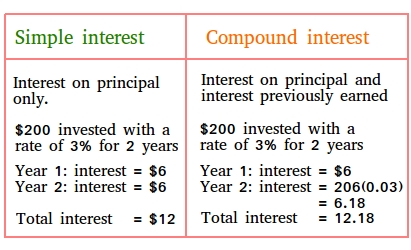
Simple vs compound interest: an example showing the difference between the two.

For example, 4000 dollars is deposited into a bank account and the annual interest rate is 8%.

How much is the interest after 4 years?

Use the following simple interest formula:

I = p × r × t, where p is the principal or money deposited

r is the rate of interest

t is time

We get:

I = p × r × t

I = 4000 × 8% × 4

I = 4000 × 0.08 × 4

I = 1280 dollars

The interest after 4 years is 1280 dollars.

However, compound interest is the interest earned not only on the original principal, but also on all interests earned previously. You are basically earning or paying interest on interest!

In other words, at the end of each year, the interest earned is added to the original amount and the money is reinvested.

If we use compound interest for the situation above, the interest will be computed as follow:

Interest at the end of the first year:

I = 4000 × 0.08 × 1

I = 320 dollars

Your new principal per say is now 4000 + 320 = 4320

Interest at the end of the second year:

I = 4320× 0.08 × 1

I = 345.6 dollars

Your new principal is now 4320 + 345.6 = 4665.6

Interest at the end of the third year:

I = 4665.6× 0.08 × 1

I = 373.248 dollars

Your new principal is now 4665.6 + 373.248 = 5038.848

Interest at the end of the fourth year:

I = 5038.848 × 0.08 × 1

I = 403.10784 dollars

Your new principal is now 5038.848 + 403.10784 = 5441.95584

Total interest earned = 5441.95584 − 4000 = 1441.95584

The difference in money between compound interest and simple interest is 1441.96 - 1280 = 161.96

As you can see, compound interest yield better result, so you make more money.

You could also use the compound interest formula shown below.

A = P(1 + r)^t

P is the principal amount and it is equal to 4000

t is the number of years 4000 is invested and it is equal to 4 in this case.

r is the interest rate and it is equal to 8%

A = P(1 + r)^t

A = 4000(1 + 0.08)⁴

A = 4000(1.08)⁴

A = 4000(1.36048)

A = 5441.92

Interest = 5441.92 - 4000

Accumulated interest = 1441.92

Simple vs compound interest when investing or borrowing money

Before investing or borrowing money, you should double-check with your local bank to see if the calculations are done using simple interest or compound interest.

As a rule of thumb,

Most savings account will use compound interest.

Bonds, especially those in the United States, will most likely use simple interest.

Savings bonds can use compound interest

Although this one may surprise you big time, mortgages use simple interest.

Car loans also use simple interest

This may come to no surprise, but student loans also use simple interest.

If you have a credit card and you owe money on it, you will pay less interest if the credit card company uses simple interest. However, they will never do something so foolish!
Borrowing money with a credit card is not cheap. Most credit cards will use compound interest and the frequency of compounding could be daily so that they can earn as much interest as possible.

Certificates of deposit also called CDs will use compound interest

I hope simple vs compound interest is well understood now!