Numbers of solutions of systems of linear equations

This lesson will examine the 3 types of solutions of systems of linear equations. A system of linear of equations can have 1 solution, no solution, or infinitely many solutions. The slopes and the y-intercepts of the lines will determine the kind of solution the system will have.

Solutions of systems of linear equations: 1 solution

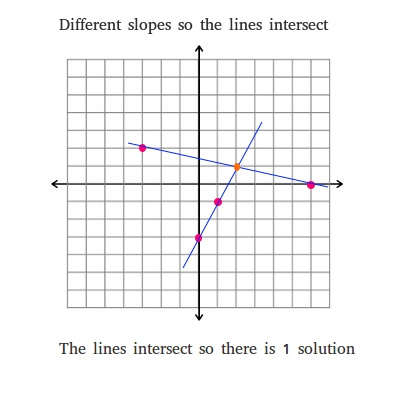
A system of linear equations has 1 solution if the lines have different slopes regardless of the values of their y-intercepts. 

For example, the following systems of linear equations will have one solution. We show the slopes for each system with blue. Notice how the slopes are different.

1.   y = (-2/9)x + 6                
      y =  2x + - 3                          

2.   y = -8x + 6
      y =  8x + -10

3.   y = 0.5x + 3
      y =   6x + 3 

If we graph the first system on the left, you can see the solution or the point of intersection with the orange dot. If you do not understand how we graphed the lines below, go to the lessons about graphing slope.

Solutions of systems of linear equations: no solution

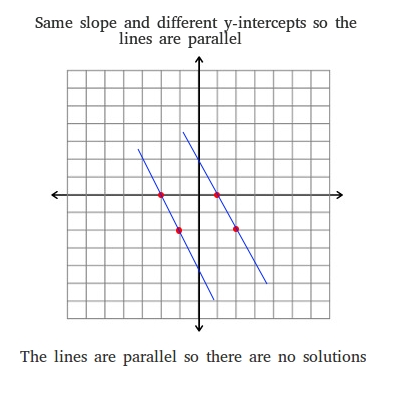
A system of linear equations has no solution if the lines have the same slope but different y-intercepts. 

For example, the following systems of linear equations will have no solution. We show the slopes for each system with red and the y-intercepts with blue. Notice how the slope is the same, but the y-intercepts are different.

4.  y =  -2x + 1           
     y =  -2x -  2                        

5.   y  =  3x + 5 
      y =  3x + -8 

6.   y =  (2/5)x + -6      
      y = (2/5)x  + 1

After graphing the fourth system, you can see that the lines are parallel.

Solutions of systems of linear equations: infinitely many solutions.

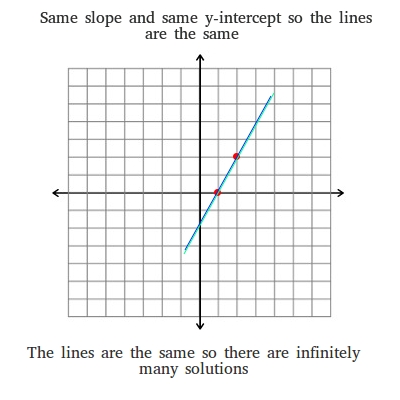
A system of linear equations has infinitely many solutions if the lines have the same slope and the same y-intercept. 

For example, the following systems of linear equations will have infinitely many solutions. Notice how the slope is the same and how the y-intercept is the same.

7.  y = 2x + 1                                        
     y = 2x + 1                         

8.   y = -4x + 1/2
      y = -4x  + 1/2 

9.  y = (3/4) x + 8
     y = (3/4)x + 8

After graphing the seventh system, we see that the two graphs meet everywhere.