Spread of a normal distribution

This lesson will show how the value of the standard deviation or σ gives the spread of a normal distribution.

Recall that in the lessons about measures of dispersion and standard deviation, we saw that the bigger the standard deviation, the bigger the spread.

Well, this may help us understand the spread of a normal distribution as well.

The following shows three normal distribution curves with the same mean but different standard deviations.

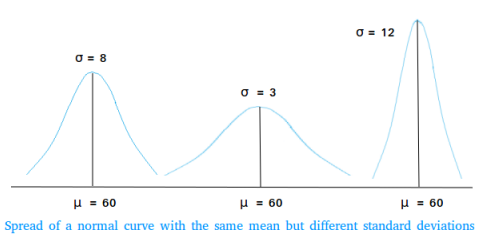
Notice that the value of μ dictates the center of a normal curve on the horizontal axis. The value of μ has nothing to do with the height of the normal curve!

As you can see in the image above, here is how it works.

The bigger the value of the standard deviation is , the bigger the spread and the smaller the height.

The smaller the value of the standard deviation is , the smaller the spread and the bigger the height.

The following shows three normal distribution curves with different means but the same standard deviation.

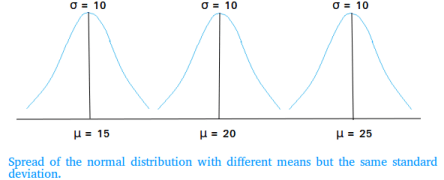
When the standard deviation is the same, the spread and the height of the normal distribution curves are the same.