Surface area formula
Here, we provide you with a comprehensive list of surface area formula for some common three-dimensional figures such as the cube, the cylinder, the rectangular prism, the sphere, the right circular cone, and the right square pyramid.
Surface area of a cube = 6 × a2
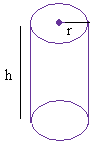
Surface area of a cylinder = areas of the two bases + lateral surface area
Surface area of a cylinder = 2 × pi × r2 + 2 × pi × r × h
pi = 3.14
h is the height
r is the radius
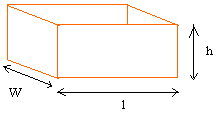
Surface area of a cuboid = 2lw + 2lh + 2wh = 2(lw + lh + wh)
Surface area of a rectangular prism = 2 × l × w + 2 × l × h + 2 × w × h
l is the length
w is the width
h is the height
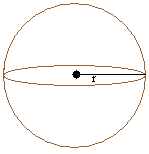
Surface area of a sphere = 4 × pi × r2
pi = 3.14
r is the radius
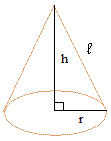
Surface area of a cone = pi × r2 + pi × r ×( √(h2 + r2))
pi = 3.14
r is the radius
h is the height
l is the slant height of the cone
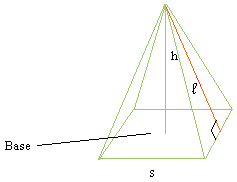
Surface area of a pyramid = s2 + 2 × s × l
s is the length of the base
h is the height
l is the slant height
Less common surface area formulas that are important to know as well.
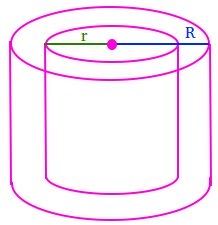
Total surface area of a hollow cylinder = 2πh(R + r) + 2π(R2 - r2)
π = 3.14
h is the height
r is the radius of the inner circle
R is the radius of the outer circle
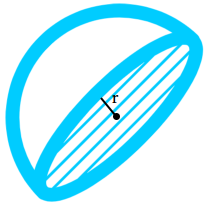
Surface area of a hemisphere = 3πr2
π = 3.14
r is the radius of the hemisphere
Examples showing how to use the surface area formula to solve some problems.
Example #1
Find the surface area of a cube if the length of one side is equal to 5 ft.
The formula to use to find the surface area of cube is 6a2
6a2 = 6 × a2 = 6 × 52 = 6 × 25 = 150
The surface area of the cube is 150 ft2
Example #2
Find the surface area of a cylinder if the diameter of the base is 10 inches and the height of the cylinder is 8 inches.
Since the radius is half the diameter, r = 10/2 = 5
The lateral area (L.A.) is 2 × pi × r × h
L.A. = 2 × pi × r × h = 2(3.14)(5)(8)
L.A. = (6.28)(40) = 251.2
The areas of the two bases is equal to 2 × pi × r2
2(3.14)(52) = 6.28(25) = 157
SA = total surface area = 251.2 + 157 = 408.5 square inches
Example #3
The dimensions of a rectangular prism are shown below
Length is equal 5 cm
Width is equal to 6 cm
Height is equal 3 cm
Find the surface area of the rectangular prism.
The formula to use to find the surface area of a rectangular prism as already shown above is 2lw + 2lh + 2wh = 2 × l × w + 2 × l × h + 2 × w × h
2 × 5 × 6 + 2 × 5 × 3 + 2 × 6 × 3
2 × 30 + 2 × 15 + 2 × 18
60 + 30 + 36
90 + 36
126
The surface area of the rectangular prism is 126 cm2
Surface Area Formula FAQs
-
We can look for the area of a flat surface such as a rectangle or a triangle. However, we look for the surface area of a solid figure such as a cube or a cylinder.
-
A cube has 6 equal faces. Each face is a square. Therefore, to get the surface area, just find the area of a square and then multiply by 6.
-
Suppose a is the length of an edge (length of one side of a face)
The formula for volume of a cube is a3 and the formula for surface area is 6a2