Area formula
The area formula is used to find the number of square units a polygon encloses. The figure below shows some area formulas that are frequently used in the classroom or in the real-world.
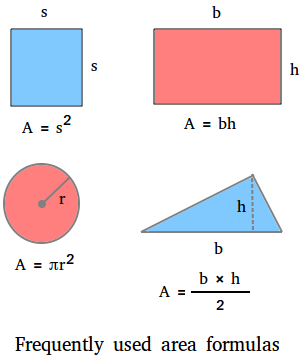
Area of a square
The area of a square is the square of the length of one side. Let s be the length of one side.
A = s2 = s × s
Area of a rectangle
The area of a rectangle is the product of its base and height.
Let b = base and let h = height
A = b × h = bh
For a rectangle, "length" and "width" can also be used instead of "base" and "height"
The area of a rectangle can also be the product of its length and width
A = length × width
Area of a circle
The area of a circle is the product of pi and the square of the radius of the circle.
Let r be the radius of the circle and let pi = π = 3.14
A = πr2
Please see the lesson about area of a circle to get a deeper knowledge.
Area of a triangle
The area of a triangle is half the product of the base of the triangle and its height.
Let b = base and let h = height
Area = (b × h)/2
Area of a parallelogram
The area of a parallelogram is the product of its base and height.
Let b = base and let h = height
A = b × h = bh
Please see the lesson about parallelogram to learn more.
Area of a rhombus
The area of a rhombus / area of a kite is half the product of the lengths of its diagonals.
Let d1 be the length of the first diagonal and d2 the length of the second diagonal.
A = (d1 × d2)/2
Area of a trapezoid
The area of a trapezoid is half the product of the height and the sum of the bases.
Let b1 be the length of the first base, b2 the length of the second base, and let h be the height of the trapezoid.
A = [h(b1 + b2)]/2
Please see the lesson about area of a trapezoid to learn more.
Area of an ellipse
The area of the ellipse is the product of π, the length of the semi-major axis, and the length of the semi-minor axis.
Let a be the length of the semi-major axis and b the length of the semi-minor axis.
A = πab
The semi-major axis is also called major radius and the semi-minor axis is called minor radius.
Let r1 be the length of the semi-major axis and r2 the length of the semi-minor axis.
The area is also equal to πr1r2
A couple of example showing how to use the area formula
Example #1
What is the area of a rectangular backyard whose length and breadth are 50 feet and 40 feet respectively?
Solution:
Length of the backyard = 50 ft
Breadth of the backyard = 40 ft
Area of the backyard = length × breadth
Area of the backyard = 50 ft × 40 ft
Area of the backyard = 2000 square feet = 2000 ft2
Example #2
The lengths of the adjacent sides of a parallelogram are 12 cm and 15 cm. The height corresponding to the 12-cm base is 6 cm. Find the height corresponding to the 15-cm base.
Solution:
A = b × h = 12 × 6 = 72 cm2
Since the area is still the same, we can use it to find the height corresponding to the 15 cm base.
A = b × h
Substitute 72 for A and 15 for b.
72 = 15 × h
Divide both sides of the equation by 15
72/15 = (15/15) × h
4.8 = h
The height corresponding to the 15 cm base is 4.8 cm.
Example #3
The diameter of a circle is 9. What is the area of the circle?
Solution:
Since the radius is half the diameter, r = 9/2 = 4.5
A = πr2
A = 3.14(4.5)2
A = 3.14(20.25)
A = 63.585