Surface area of a cone

The surface area of a cone can be derived from the surface area of a square pyramid.

Start with a square pyramid and just keep increasing the number of sides of the base. After a very large number of sides, you can see that the figure will eventually look like a cone.This is shown below:


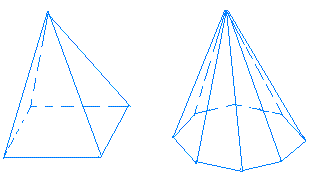
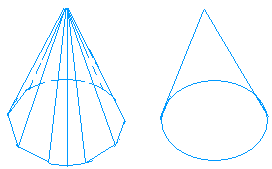
This observation is important because we can use the formula of the surface area of a square pyramid to find that of a cone.

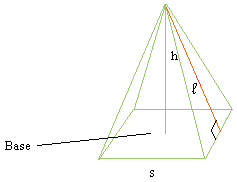
l is the slant height.

The area of the square is s²

The area of one triangle is (s × l)/2

Since there are 4 triangles, the area is 4 × (s × l)/2 = 2 × s × l

Therefore, the surface area, call it SA is:

SA = s²  +  2 × s × l .

Generally speaking, to find the surface area of any regular pyramid where A is the area of the base, the perimeter is P, and the slant height is l, we use the following formula:

S = A + 1/2 (P × l)

Again A is the area of the base. For a figure with 4 sides, A = s² with s = length of one side.

Where does the 1/2 (P × l) come from?

Let s be the length of the base of a regular pyramid. Then, the area of one triangle is (s × l)/2

For n triangles and this also means that the base of the pyramid has n sides, we get ( n × s × l)/2

Now P = n × s. When n = 4, of course, P = 4 × s as already shown.

Therefore, after replacing n × s by P, we get S = A + 1/2 (P × l)

Let us now use this fact to derive the formula of the surface area of a cone

How to derive the formula to get the surface area of a cone?

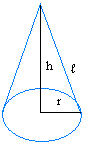
For a cone, the base is a circle, so A = π × r²

P = 2 × π × r

To find the slant height, l, just use the Pythagorean Theorem

l = r² + h²

l = √ (r² + h²)

Putting it all together, we get:

S = A + 1/2 (P × l)

S = π × r² + 1/2 ( 2 × π × r × √ (r² + h²)

S = π × r² + π × r × √ (r² + h²)

3 examples showing how to find the surface area of a cone.

Example #1:

Find the surface area of a cone with a radius of 4 cm, and a height of 8 cm

S = π × r² + π × r × √ (r² + h²)

S = 3.14 × 4² + 3.14 × 4 × √ (4² + 8²)

S = 3.14 × 16 + 12.56 × √ (16 + 64)

S = 50.24 + 12.56 × √ (80)

S = 50.24 + 12.56 × 8.94

S = 50.24 + 112.28

S = 162.52 cm²

Example #2:

Find the surface area of a cone with a radius of 9 cm, and a height of 12 cm

S = π × r² + π × r × √ (r² + h²)

S = 3.14 × 9² + 3.14 × 9 × √ (9² + 12²)

S = 3.14 × 81 + 28.26 × √ (81 + 144)

S = 254.34 + 28.26 × √ (225)

S = 254.24 + 28.26 × 15

S = 254.24 + 423.9

S = 678.14 cm²