System of Linear Equations
System of linear equations can arise naturally from many real life examples. Generally speaking, those problems come up when there are two unknowns or variables to solve.
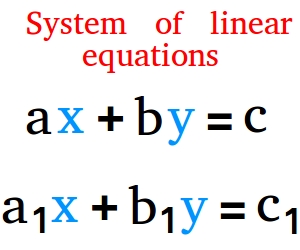
In the figure above, there are two variables to solve and they are x and y. This kind of system is called system of linear equations with 2 variables.
Real-life situations that lead to a system of linear equations
Example #1
The sum of two numbers is twenty and their difference is ten. What are the two numbers?
Here is how to set up the system:
Let x be the first number
Let y be the second number
Then,
x + y = 20
x − y = 10
You can also write:
x + y = 20
y − x = -10
You will get the same answers!
Example #2
You have 24 coins in your pockets that are worth 4.50 dollars. How many coins are quarters? How many coins are dimes?
Here is how to set it up:
Let q be the number of quarters.
Let d be the number of dimes.
Then,
q + d = 24
25 × q + 10 × d = 450
The second equation is tricky. How did we get it?
Since 1 quarter equal to 25 cents, q quarter equal to 25 × q.
If you had 6 quarters and you wanted to know how many cents are there for the 6 quarters, would you not do 6 × 25?
Just say to yourself that now instead of 6 quarters you have q quarters. Does that make sense?
In a similar way, since 1 dime equal to 10 cents, d dimes equal 10 × d.
What about the 450? 4.50 dollars times 100 = 450 cents.
Finally, since 25 × q represents how many cents you have for quarters and 10 × d represents how many cents you have for dimes, adding them should equal to the total of 450 cents.
Example #3
A cell phone plan offers 300 free minutes for a flat fee of 20 dollars. If your usage exceed 300 minutes, you pay 50 cents for each minute.
A second cell phone plan offers 500 free minutes for a flat fee of 30 dollars. If your usage exceed 400 minutes, you pay 25 cents for each minute.
Model the cost of both plan with a system.
Here is how to set up the system:
Let x be the number of minutes you talk.
Let y be the cost.
y = 20 + 0.50 (x - 300)
y = 30 + 0.25 (x - 500)
y = 20 + 0.50x - 150
y = 30 + 0.25x - 125
Subtract 0.50x from both sides of the first equation and subtract 0.25x from both sides of the second equation.
We get:
y − 0.50 x = 20 - 150
y − 0.30 x = 30 - 125
y − 0.50 x = -130
y − 0.30 x = -95
Have Great System of Linear Equations Word Problem?
Type the problem and show us how you solve it!
Other system of linear equations visitors have solved.
Click below to see contributions from other visitors to this page...
Solve real world problems with a system of linear equations 




A burger place sells burgers (b) for $4, and fries (f) for $2. If bob bought six items for a total of $18, how many did he buy of each?
Solution …
Solving system of linear equations by substitution 




y = 2x
x + y = 21
Replace y = 2x into the second equation.
we get:
x + 2x = 21
we get
3x = 21
divide both sides of the equation by …
Solve a system of linear equations to find the cost of a cd 




Andrew had $93.00. With this money, he could buy 3 CDs and 4 books. However, he bought only 2 CDs and 3 books and had $27.00 left. What was the cost …
Solving an Age Problem with a System of Linear Equations 




The sum of Mira and Shaheena is 40 years. After 10 years Mia will be twice as old as Shaheena. What is Mia's age. What is Shaheena's age?
Solution …
Solving a word problem with 3 unknowns using a linear equation 




Amanda, Henry, and Scott have a total of $89 in their wallets. Amanda has $6 less than Scott. Henry has 3 times what Scott has. How much does each have? …
Write and solve a system of linear equations to find the length and the width of a rectangle 




The perimeter of a rectangle is 138 inches. The length exceeds the width by 65 inches. Find the length and width.
Solution
P = 2l + 2w
l = w …
Age and system of linear equations 




Alvin's age is three times Elga's age. The sum of their ages is " 40 ". What is Elga's age?
Let x be Alvin's age
Let y be Elga's age
x + y = …
Rectangle word problem 




The length of a rectangle is 5 more than the width and the area is 24. Find the length and the width.
Solution
The formula of the area of a rectangle …
Story word Problem: linear equation 




A salesperson earns $200 per week in base pay plus one-twentieth of his/her dollar sales volume. Find the salesperson’s dollar sales volume if he/she …
Solving a system of linear equations when the lines are parallel 




Find the value of k so that the two given lines will be parallel.
3X-KY=7
2X+5Y=-1
First, put the two equations in standard form
3X - KY = 7 …
Selling lemonade word problem 




Sasha and Francisco were selling lemonade for 25 cents per half cup and 50 cent per full cup. At the end of the day they had collected 17 dollars and had …
Mixture word problem 


A scientist wants to dilute a 60% acid solution by adding some 20% solution. If she starts with 80 ml of the 60% solution, how many milliliters of the …
Solve a simple system with five equations Not rated yet
The sum of four numbers a, b, c, and d is 68. If we increase a by 7, we get x. If we increased b by 8, we get x. If we decrease c by 15, we get 2x.If we …
Speed word problem Not rated yet
A truck left a depot at noon traveling an average speed of 40 kilometers per hour. How far from the depot and what time will it overtake another truck, …
Apartment Word Problem Not rated yet
In an apartment building some apartments have a one bedroom and the rest have two bedrooms if there are a total of 50 apartments and 80 bedrooms how many …
Find each side of a triangle Not rated yet
The perimeter of a triangle is 58 centimeters. The longest side is 2 centimeters less than the sum of the other two sides. Twice the shortest is 12 centimeters …