Tension word problems

To solve these tension word problems, you will mostly need Newton's second law of motion.  

Problem # 1

a 100 kg bucket  is being lifted by a rope. The bucket started at rest and after being lifted 4 m, it is moving at 4 m/s. If the acceleration is constant, what is the tension on the rope?

Solution

The diagram below describes the problem and it is useful in order to visualize the problem.

Tension word problem

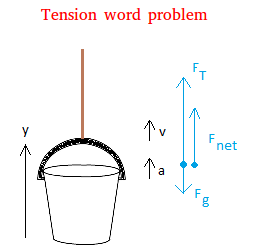
Observations:

FT is the force of tension and it is represented with a bigger vector. This force has to be bigger since it is making the bucket go up.

The bucket started from rest, so V0 = 0

Then the bucket moved with a speed of 4 m/s, so V = 4 m/s

Fg is the force of gravity

The positive direction is chosen to be up

Fnet = FT - Fg

FT = Fnet + Fg

FT = m × a + m × g

FT = m × (a + g)

The only missing quantity is a. To get a, we can use one of the constant acceleration equations.

Since we know V0, V, and d, we can use V2 = V02 + 2ad

42 = 02 + 2 × a × 4

16 = 0 + 8a

16 = 8a

a = 2 m/s2

FT = 100 × (2 + 9.8)

FT = 100 × 11.8 = 1180 Newtons

Problem # 2:

A rope is attached to a vehicle weighing 500 kN. A very strong man puts the other end of the rope inside his mouth at an angle of 30 degrees from the horizontal. If the strong man is able to move the vehicle with a constant force 1 m away with a speed of 0.25 m/s, what is the tension on the rope. (Use g = 10 m/s2) 

Solution

This situation is shown below with graph.

Tension word problem

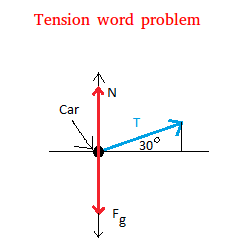
Newton's second law gives F = ma

Since the vehicle is only moving along the x axis, the only force on the vehicle is along the x axis.

We get Fx = max

The force Fx that we need here is the horizontal component of the tension force.

cos(30°) =
Tx / T

Tx = T cos(30°)

T cos(30°) = max

We need to find the acceleration and the mass of the vehicle.

m =
W / g

m =
500000 / g

m =
500000 / 10
= 50000 kg

Since the man is moving the vehicle with a constant force, the acceleration is constant. Therefore, we can use the following equation again to get the acceleration.

V2 = V02 + 2ad

0.252 = 02 + 2 × a × 1

0.0625 = 0 + 2a

0.0625 = 2a

a = 0.03125 m/s2

We can now find the tension on the rope

T cos(30°) = max

T cos(30°) = 50000 × 0.03125

T cos(30°) = 1562.5

T × 0.866 = 1562.5

T = 1562.5 / 0.866

T = 1804.27 Newtons

Tension word problems and constant acceleration equations

Notice how important it was to use one of the constant acceleration equations to solve the two tension word problems above. Many problems in physics have a constant acceleration. Therefore, try to become familiar to these equations since they will keep coming back when solving word problems.