Triangle inequality theorem proof

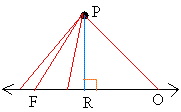
Before you understand the triangle inequality theorem proof, you need to review the triangle inequality theorem and understand the shortest distance theorem.

Shortest distance theorem:

The shortest distance from a point p to a line s is the line perpendicular to s and passing through p.

This is illustrated below. As you can see the shortest distance is segment PR and this is shown in blue.

Any other segments such as segment PF or segment PO ( shown in red) is longer.

You have to understand this theorem before trying to comprehend the proof about triangle inequality theorem.

Suppose you have a triangle ABC. The proof must have the following 3 parts.

BA + AC > BC

BA + BC > AC

BC + AC > BA

In this lesson, we will prove that BA + AC > BC and BA + BC > AC. 

It will be up to you to prove that BC + AC > BA

Now, here is the triangle inequality theorem proof

Draw any triangle ABC and the line perpendicular to BC passing through vertex A. (This is shown in blue)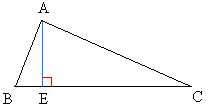



Now prove that BA + AC > BC.

BE is the shortest distance from vertex B to AE.

This means that BA > BE.

By the same token,

CE is the shortest distance from C to AE.

This means that AC > CE.

Let us put it all together:

BA > BE and

AC > CE

Add the left side and add the right side of the inequalities. This gives:

BA + AC > BE + CE

Now, notice that BE + CE = BC

Therefore, BA + AC > BC

Now, starting with the same triangle, draw the line perpendicular to AC passing through vertex B. (This is shown in blue)




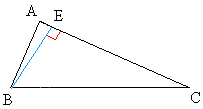
Prove that BA + BC > AC

AE is the shortest distance from vertex A to BE

This means that BA > AE

By the same token,

CE is the shortest distance from C to BE

This means that BC > CE

Let us put it all together:

BA > AE and

BC > CE

Add the left side and add the right side of the inequalities. This gives:

BA + BC > AE + CE

Now, notice that AE + CE = AC

Therefore, BA + BC > AC

Now, here is your exercise: Try to prove that AC + BC > AB