Triangle inequality theorem

The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side. Look at the figure below carefully.

Did you notice what we did with the triangle ?



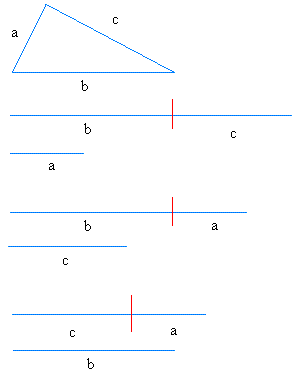
First, we removed the three sides.

Next, we paired them by putting one side next to the other and compared each pair with the third side.

What did you noticed about the length of each pair?

The length of each pair is always bigger than the length of the third side.

The above is a good illustration of the inequality theorem.

Given any triangle, if a, b, and c are the lengths of the sides, the following is always true:

a + b > c

a + c > b

b + c > a

How to use the triangle inequality theorem to find out if you can make a triangle when three sides or lengths are given.

The triangle inequality theorem is very useful when one needs to determine if any 3 given sides will form of a triangle or not.

In other words, suppose a, b, and c are the lengths of the sides of a triangle. If the 3 conditions below are not met, you can immediately conclude that it is not a triangle.

a + b > c

a + c > b

b + c > a

Example #1:

Three segments have lengths a = 3 cm, b = 6 cm, and c = 4 cm. Can a triangle be formed with these measures?

3 + 6 = 9 and 9 > 4

3 + 4 = 7 and 7 > 6

6 + 4 = 10 and 10 > 3

So, yes, a triangle can be formed with these three measures!

Example #2:

Three segments have lengths a = 7 cm, b = 16 cm, and c = 8 cm. Can a triangle be formed with these measures?

7 + 16 = 23 and 23 > 8

7 + 8 = 15 , but 15 < 16. This condition is not met because the sum of these two sides is smaller than the third side.

16 + 8 = 24 and 24 > 7

Since one of the conditions is not met, a triangle cannot be formed with these three measures.