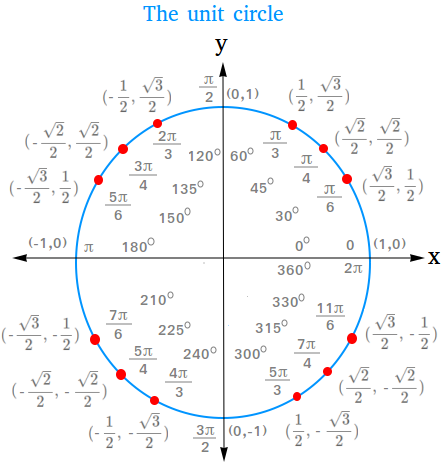
Definition of the unit circle

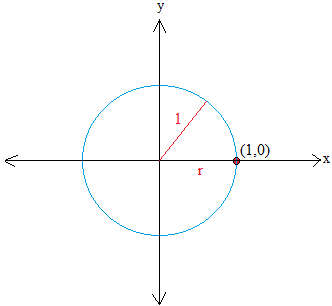
A unit circle is a circle whose radius is equal to 1. Furthermore, the circle has its center at the origin of a rectangular coordinate system.

Let P = (x , y) be a point on the circle. Then, make a right triangle by drawing a line perpendicular to x. The line is shown in green.

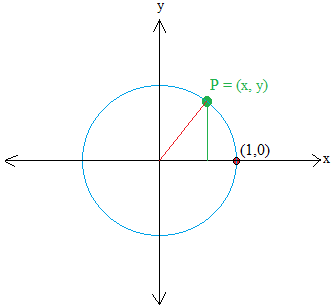
The horizontal leg of the triangle is x units away from the origin and the vertical leg of the triangle is y units away from the origin.

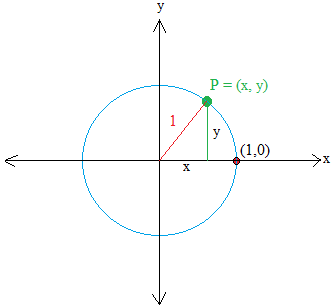
Using the Pythagorean theorem, we get x² + y² = 1² or x² + y² = 1

We can take a step further so we can derive an important trigonometric function. Let us name θ the angle made with the radius in red and the x axis.

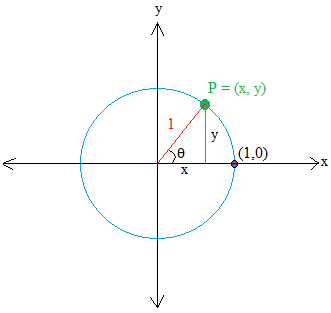
Take a close look at the triangle and you will see as we learned before that the adjacent side to angle θ is x and the opposite side is y.

Therefore, sinθ = y / 1 = y and cosθ = x / 1 = x

sinθ is read as sine of θ and sinθ is the y-coordinate of point P.

cosθ is read as cosine of θ and cosθ is the x-coordinate of point P.

We can replace x = cosθ and sinθ in x² + y² = 1

We get (cosθ)² + (sinθ)² = 1 or cos²θ + sin²θ = 1

Definitions of the six trigonometric functions in terms of the unit circle.

cosθ = x

secθ = 1/x, with x not equal to 0 (secθ is the reciprocal of cosθ)

sinθ = y

cscθ = 1/y, with y not equal to 0 (cscθ is the reciprocal of sinθ)

tanθ = y/x, with x not equal to 0

cotθ = x/y, with y not equal to 0 (cotθ is the reciprocal of tanθ)

We can also call the six trigonometric functions above circular functions because of the fact that we are using a unit circle to express the functions values.

We just derived some of the most important trigonometric functions. We have just scratched the surface of what we can do with the unit circle. Now we need to complete the unit circle with the most important trigonometric values

How to find trigonometric values using the unit circle

The two lessons using the unit circle to find sin(45 degrees) and cos(45 degrees) and using the unit circle to find the cosine and sine of 30 and 60 degrees angles will show how you can use the unit circle to find the following important trigonometric values.

sin 45 degrees = √(2) / 2

cos 45 degrees = √(2) / 2

cos(30 degrees) = √3 / 2

cos(60 degrees) = 1 / 2

sin(60 degrees) = √3 / 2

sin(30 degrees) = 1 / 2

Since the values above are positive numbers, they will go in the first quadrant of the unit circle. We will also put each value on the unit circle as a point (x, y).

Recall that from the previous section, we saw that cosθ = x and sinθ = y

(x, y) = (cosθ, sinθ)

You will then have these points in the first quadrant.

(cos 30 degrees, sin 30 degrees) = (√3 / 2, 1 / 2)

(cos 45 degrees, sin 45 degrees) = (√2 / 2, √2 / 2)

(cos 60 degrees, sin 60 degrees) = (1 / 2, √3 / 2)

Unit circle and trigonometric values in the first quadrant

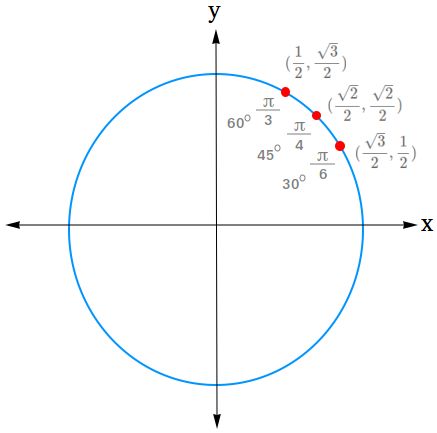
Notice that in radians,

30 degrees is equal to π/6 rad

45 degrees is equal to π/4 rad

60 degrees is equal to π/3 rad

Now, we need to find more trigonometric values in quadrant II, quadrant III and quadrant IV.

Quadrant II

The points in the second quadrant we are looking for will be symmetric to the three points in the first quadrant with respect to the y-axis. The y-value is positive, but the x-value is negative.

The point symmetric to 60 degrees has an angle that is equal to 120 degrees (60 + 30 + 30)

The point symmetric to 45 degrees has an angle that is equal to 135 degrees (45 + 45 + 45)

The point symmetric to 30 degrees has an angle that is equal to 150 degrees (30 + 30 + 30 + 30 + 30)

You will then have these points in the second quadrant.

(cos 120 degrees, sin 120 degrees) = (-1 / 2, √3 / 2)

(cos 135 degrees, sin 135 degrees) = (-√2 / 2, √2 / 2)

(cos 150 degrees, sin 150 degrees) = (-√3 / 2, 1 / 2)

Quadrant III

The points in the third quadrant are symmetric to the three points in the second quadrant with respect to the x-axis. The y-value is negative and the x-value is negative.

The point symmetric to 120 degrees has an angle that is equal to 240 degrees (120 + 60 + 60)

The point symmetric to 135 degrees has an angle that is equal to 225 degrees (135 + 45 + 45)

The point symmetric to 150 degrees has an angle that is equal to 210 degrees (150 + 30 + 30)

You will then have these points in the third quadrant.

(cos 240 degrees, sin 240 degrees) = (-1 / 2, -√3 / 2)

(cos 225 degrees, sin 225 degrees) = (-√2 / 2, -√2 / 2)

(cos 210 degrees, sin 210 degrees) = (-√3 / 2, -1 / 2)

Quadrant IV

The points in the fourth quadrant are symmetric to the three points in the third quadrant with respect to the y-axis. The y-value is negative and the x-value is positive.

The point symmetric to 240 degrees has an angle that is equal to 300 degrees (240 + 30 + 30)

The point symmetric to 225 degrees has an angle that is equal to 315 degrees (225 + 45 + 45)

The point symmetric to 210 degrees has an angle that is equal to 330 degrees (210 + 60 + 60)

You will then have these points in the fourth quadrant.