Using the unit circle to find sin(45 degrees)

Now that you are familiar with the unit circle, let us show you that just like the right triangle, the unit circle can be used to find sin(45 degrees) and also cos(45 degrees)

In the lesson about tangent ratio and sine ratio, we also used a 45 degrees triangle.

What do you remember about the lengths of the legs ?

For a right triangle that has a 45 degrees angle, the legs have the same length.

This means that x = y.

We can again use the Pythagorean theorem to find x and y.

x² + y² = 1²

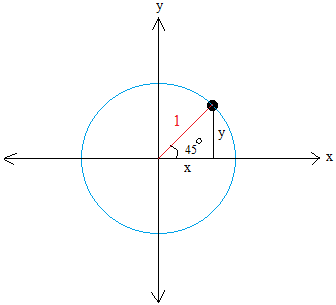
x² + y² = 1

Since x = y, we get:

x² + x² = 1

2x² = 1

Divide both sides by 2

x² = 1 / 2

x = √(1 / 2)

x = √(1) / √(2)

x = 1 / √(2)

Since x = y, y is also equal to 1 / √(2)

cos(45 degrees) = x / 1 = x

sin(45 degrees) = y / 1 = y

Therefore,

cos(45 degrees) = 1 / √(2)

sin(45 degrees) = 1 / √(2)

Using the unit circle to find sin(45 degrees) versus using the right triangle.

We can see that whether we use the right triangle only or the unit circle, we get the same answer. Since trigonometry means the measurement of triangles, you may have wondered so far why we use the unit circle to do trigonometry. Again, we get the same answer. Moreover, using the right triangle only has its limitations. 

With the right triangle only, all angles must be positive while with the unit circle, angles could be negative. 

Some values are hard to find with the right triangle although not impossible. For example, using the triangle below, what is sin (90 degrees) or cos(90 degrees)?

You could do what this teacher is doing on this video to find these values. However, since his method involves an imaginary angle of 0 degrees and as a result, this figure is no longer a triangle, you are better off using the unit circle.

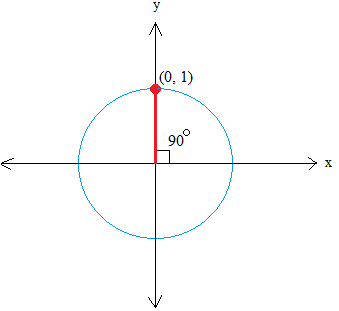
On the unit circle, the sine of any angle is equal to the y-value, so sin(90 degrees) = 1

Similarly, the cosine of any angle is equal to the x-value, so cos(90 degrees) = 0