Volume formulas

Here, we provide you with volume formulas for some common three-dimensional figures and also for the ellipsoid and the hollow cylinder that are not so common.

Cube:

Volume = a³ = a × a × a

Cylinder:

Volume = π × r² × h

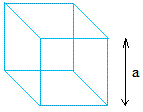
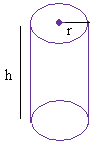
π = 3.14
h is the height
r is the radius

Rectangular solid or cuboid:

Volume = l × w × h

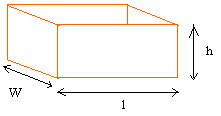
l is the length
w is the width
h is the height

Sphere:

Volume = (4 × π × r³)/3

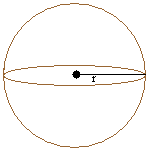
π = 3.14
r is the radius

Cone:

Volume = (π × r² × h)/3

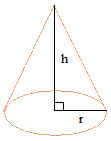
pi = 3.14
r is the radius
h is the height

Pyramid:

Volume = (B × h)/3

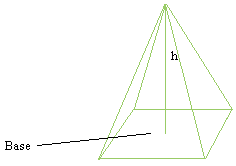
B is the area of the base
h is the height

Less common volume formulas

Ellipsoid:

Volume = (4 × π × a × b × c)/3

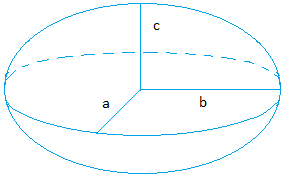
Use π = 3.14

Hollow cylinder:

Volume = π × R² × h - π × r² × h

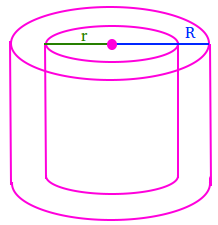
Volume = π × h ( R² - r²)

Use π = 3.14.

How to use the volume formulas to calculate the volume

Volume of a cube 

The length of a side = a = 2 cm

Volume = (2 cm) = 2 cm × 2 cm × 2 cm = 8 cm³ = 8 cubic centimeters 

Volume of a cylinder

The height is 8 inches and the radius is 2 inches.

Volume = π × r² × h = 3.14 × (2 in)² × 8 in = 3.14 × 4 × 8 in³
Volume = 3.14 × 32 in³ = 100.48 in² = 100.48 cubic inches 

Volume of a cuboid or rectangular solid 

The length is 6 cm, the width is 3 cm and the height is 5 cm.

Volume = l × w  × h =  6 × 3 × 5 = 90 cm³ = 90 cubic centimeters

Volume of a sphere 

The radius = r = 20 

Volume = (4 × π × r³)/3 = [4 × 3.14 × (20)³]/3 = 3.14 × (20)³ × 4
Volume = 3.14 × 8000 × 4 = 3.14 × 32000 = 100480

Volume of a cone 

The radius is equal to 3 and the height is equal to 4.

Volume = (π × r² × h)/3 = [3.14 × (3)²× 4]/3 = 3.14 × 9 × 4
Volume = 3.14 × 36 = 113.04

Volume of a pyramid

A pyramid has a height of 6 feet. If the base of a pyramid is a square with a length of 2 feet, find the volume.

Volume = (B × h)/3

B = area of base  = 2 ft × 2 ft = 4 ft²
Volume = (4 × 6)/3 ft³ = 24/3 ft³ = 8 ft³ = 8 cubic feet

Volume of an ellipsoid

The radii of an ellipsoid are 1 cm, 2, cm, and 3 cm.

Volume = (4 × π × a × b × c)/3 = (4 × 3.14 × 1 × 2 × 3)/3
Volume = ( 3.14 × 4 × 6)/3 = ( 3.14 × 24)/3 = 81.64/3 = 25.12 cm³ = 25.12 cubic centimeters 

Volume of a hollow cylinder

The outer radius is 8, the internal radius is 6, and the height is 10.

Volume = π × h ( R² - r²) = π × 10 ( 8² - 6²) = π × 10 ( 64 - 36)

Volume = π × 10(28) = π × 280 = 879.2

General formula to find the volume of prisms such as triangular prisms or rectangular prisms

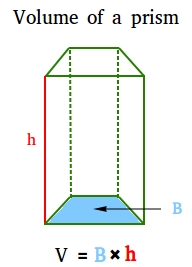
The volume of a prism is the product of the area of a base and the height of the prism.

V = Bh

A couple of examples showing how to find the volume of prisms

A triangular prism

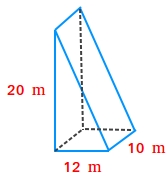
1. Find the volume of the triangular prism shown in the image above using the formula below.

V = Bh

The dimensions of the triangular base are 12 m and 20 m.

The height of the triangular prism is h = 10 m.

B = area of the triangular base  = (20 times 12)/2  = 240/2 = 120 m²

V = 120 times 10 = 1200

The volume of the triangular prism is 1200 cubic meters.

A trapezoidal prism

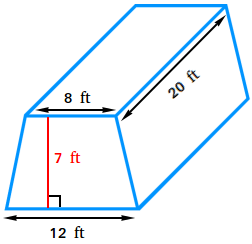
2. Find the volume of the trapezoidal prism shown in the image above using the formula below.

V = Bh

The base of the trapezoidal prism is a trapezoid with the following dimensions.

b₁ = 12 ft, b₂ = 8 ft, and height = 7 feet.

The height of the trapezoidal prism is the perpendicular distance or 20 ft

B = area of the base = [(b₁ + b₂)h]/2

B = [(12 + 8)7]/2

B = [(20)7]/2

B = 140/2

B = 70 square feet

V = 70 times 20 = 1400

The volume of the trapezoidal prism is 1400 cubic feet