45-45-90 Triangle
A 45-45-90 triangle, also called isosceles right triangle, is a special right triangle in which both legs are congruent and the length of the hypotenuse is the square root of two times the length of a leg.
Hypotenuse = √2 × length of a leg
The legs are congruent
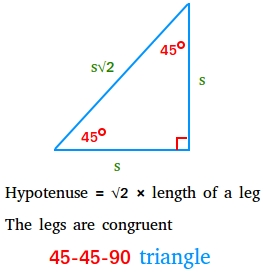
Looking carefully at the figure above, you may have observed the following ratios:
Suppose we start from the smallest angle to the largest angle and from the shortest side to the longest side
The angles of a 45-45-90 triangle are in the ratio 1:1:2
The sides of a 45-45-90 triangle are in the ratio 1:1:√2
45-45-90 triangle proof
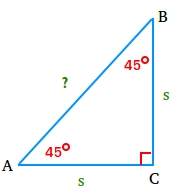
Start with an isosceles right triangle ABC like the one shown above.
Let segment AB equal to x and use the Pythagorean theorem to find the length of segment AB.
AB2 = AC2 + BC2
x2 = s2 + s2
x2 = 2s2
x = √(2s2)
x = (√2)[√(s2)]
x = (√2)(s)
x = s√2
Examples of 45-45-90 triangles
Example #1: 1, 1, √2
Each leg is equal to 1
Hypotenuse: √2
Example #2: 2, 2, 2√2
Each leg is equal to 2
Hypotenuse: 2√2
Example #3: 3, 3, 3√2
Each leg is equal to 3
Hypotenuse: 3√2
Using the length of one side to solve a 45-45-90 triangle
Example #4:
The hypotenuse of a 45-45-90 triangle is 7√2. Find the lengths of the other sides.
Hypotenuse = s√2, s is the length of a leg.
7√2 = s√2
Divide both sides by √2.
7√2 / √2 = s√2 / √2
7 = s
The legs of this 45-45-90 triangle have a length of 7
Example #5:
The legs of a 45-45-90 triangle have a length of 13. Find the length of the hypotenuse.
Hypotenuse = s√2, s is the length of a leg.
The length of the hypotenuse is 13√2
Using the 45-45-90 triangle to solve real-world problems
Example #6:
The distance from first base to second base of a baseball field is usually 90 feet although this distance may vary. Find the distance from home plate to the second base.
The distance x from home plate to the second base is the length of the hypotenuse of a 45-45-90 triangle as shown in the figure below.
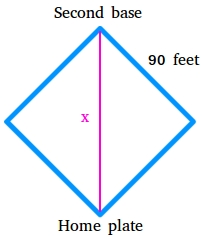
Hypotenuse = s√2, s is the length of a leg.
Since the distance from first base to second base is 90 feet, s is the length of the leg of the 45-45-90 degree triangle.
Hypotenuse = s√2
Hypotenuse = 90√2
Hypotenuse = 127.278
The distance from home plate to the second base is 127.278 feet.
Example #7:
A gardener wants to make a square garden whose diagonal is equal to 45√2 feet . What is the perimeter of the garden?
First, you need to find the length of each side of the square using the formula below.
Hypotenuse = s√2, s is the length of a leg.
45√2 = s√2
Divide both sides by √2 to find the s
45√2 / √2 = s√2 / √2
s = 45 feet
The length of each side is 45 feet.
The perimeter of the square is 45 + 45 + 45 + 45 = 90 + 90 = 180
The perimeter of the square is 180 feet.
Area of a 45-45-90 triangle
Finding the area of a 45-45-90 triangle is very straightforward. If s is the length of a leg, then, the area of a 45-45-90 triangle is s2
Example #8:
Find the area of a 45-45-90 triangle if the length of a leg is 25√3
Area = s2 = (25√3)2
Area = (25)2(√3)2
Area = 625(√3)(√3)
Area = 625(√9)
Area = 625(3)
Area = 1875