Exponential function
An exponential function is a function with the general form f(x) = y = abx and the following conditions:
- x (input value) is a real number
- a is a constant and a is not equal to zero (a ≠ 0)
- b is bigger than zero (b > 0)
- b is not equal to 1 (b ≠ 1)
- y (output value) is a positive real number
Notice the use of the independent variable (x) as an exponent. This is important in order to have an exponential function. The input value must be an exponent!
Why a cannot be equal to 0?
If a = 0, then y = 0 × bx = 0 since zero times anything is zero.
Therefore, a cannot be zero since it will make the function equal to zero.
Why b must be bigger than zero?
In other words, b cannot be zero and b cannot be a negative number.
b cannot be zero since y will be equal to a × 0x = a × 0 = 0
b cannot be negative either. This can create some problems. For example, suppose b = -1, we get y = a (-1)x
When x = 0.5, y = a(-1)0.5 = a √(-1) and √(-1) is a complex number.
Why b cannot equal to 1?
If b = 1, then y = a × 1x = a × 1 = a since 1 to any power is equal to 1 and a times 1 is a.
Notice that x disappears as an exponent when b = 1. Therefore, b cannot be equal to 1.
When b > 1, you can model growth and b is the growth factor.
When 0 < b < 1, you can model decay and b is the decay factor.
Examples of exponential functions
1. y = 0.5 × 2x
2. y = -3 × 0.4x
3. y = ex
4. y = 10x
5. y = 8(1/5)x
Can you tell what b equals to for the exponential functions above? Which functions model growth? Which functions model decay?
For 0.5 × 2x, b = 2
For y = -3 × 0.4x, b = 0.4
For ex, b = e and e = 2.71828
For 10x, b = 10
y = 8(1/5)x, b = 1/5
Therefore, if you graph 0.5 × 2x, ex, and 10x, the resulting graphs will show exponential growth since b is bigger than 1.
However, if you graph -3 × 0.4x and 8(1/5)x the resulting graph will show exponential decay since b is between 0 and 1.
What does the graph of an exponential function look like?
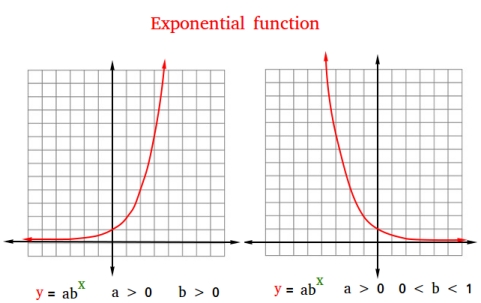
As you can see from the figure above, the general shape or graph of an exponential function can either show a growth or a decay.
If there is exponential growth, as shown in the figure on the left, the graph will curve upward. A real life example of exponential growth is population growth.
If there is exponential decay, as shown in the figure on the right, the graph will curve downward. A real life example of exponential decay is radioactive decay.
The graph crosses the y-axis, but not the x-axis.
Properties of the exponential function
If y = abx, a > 0 b > 0, the exponential graph has the following properties:
The graph is increasing
Domain and range
The domain is all real numbers or (-∞, ∞)
The range is all positive real numbers (0, ∞)
End behavior
As x approaches negative infinity, the graph will get closer and closer to the x-axis. Therefore, the graph has a horizontal asymptote that is equal to y = 0.
As x approaches positive infinity, the graph will increase without bound. This means that y will also approach infinity.
Intercepts
The x-intercept does not exist since the graph never crosses x-axis.
The y-intercept is (0,a) since y = ab0 = a(1) = a. For example, if the exponential function is y = 3x, the y-intercept is (0,1).
If y = abx, a > 0 0 < b < 1, the exponential graph has the following properties:
The graph is decreasing
Domain and range
The domain is all real numbers or (-∞, ∞)
The range is all positive real numbers (0, ∞)
End behavior
As x approaches negative infinity, the graph will increase without bound. This means that y will also approach infinity.
As x approaches positive infinity, the graph will get closer and closer to the x-axis. Therefore, the graph has a horizontal asymptote that is equal to y = 0.
Intercepts
The x-intercept does not exist since the graph never crosses x-axis.
The y-intercept is (0,a) since y = ab0 = a(1) = a. For example, if the exponential function is y = 3x, the y-intercept is (0,1).
Transformations of exponential functions
Let c be a positive real number. There are basically 5 types of transformations that can happen with exponential functions using f(x) = bx as the parent function.
- Vertical translation
- Horizontal translation
- Reflection
- Vertical stretching or shrinking
- Horizontal stretching or shrinking
The vertical translation or vertical shift occurs when the constant c is added to or subtracted from the parent function.
If c is added to the parent function, then bx + c shifts the graph of f(x) upward c units.
If c is subtracted from the parent function, then bx - c shifts the graph of f(x) downward c units.
The horizontal translation or horizontal shift occurs when the constant c is added to or subtracted from the input value of the parent function.
If c is added to the input value of the parent function, then bx+c shifts the graph of f(x) to the left c units.
If c is subtracted from the input value of the parent function, then bx-c shifts the graph of f(x) to the right c units.
Reflection occurs either with respect to the x-axis or the y-axis.
If you take the opposite of the parent function, then -bx reflects the graph of f(x) about the x-axis.
If you take the opposite of the input value of the parent function, then b-x reflects the graph of f(x) about the y-axis.
The vertical stretch occurs when the constant c is multiplied by the parent function.
If c is bigger than 1 and c is multiplied by the parent function, then cbx vertically stretches the graph of f(x).
If 0 < c < 1 and c is multiplied by the parent function, then cbx vertically shrinks or compresses the graph of f(x).
The horizontal stretch occurs when the constant c is multiplied by the input value of the parent function.
If c is bigger than 1 and c is multiplied by the input value of the parent function, then bcx horizontally shrinks the graph of f(x).
If 0 < c < 1 and c is multiplied by input value of the parent function, then bcx horizontally stretches the graph of f(x).