What is exponential growth?
What is exponential growth? Whenever a quantity is increasing or growing rapidly as a result of a constant rate of growth applied to it, that quantity is experiencing exponential growth.
The figure below is an example of exponential growth. In fact, it is the graph of the exponential function y = 2x
The general form of an exponential function is y = abx. Therefore, when y = 2x, a = 1 and b = 2.
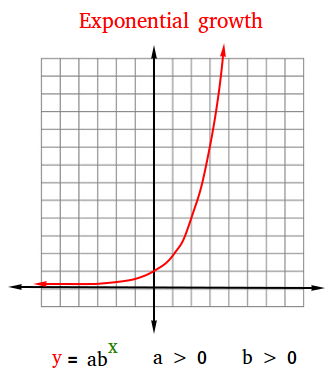
Notice that the curve looks like the letter J. For this reason, we say that exponential growth will produce a J-shaped curve.
The following table shows some points that you could have used to graph this exponential growth. Try to locate some of these points on the graph!
| x | 2x | y |
| 1 | 21 | 2 |
| 2 | 22 | 4 |
| 3 | 23 | 8 |
| 0 | 20 | 1 |
| -1 | 2-1 | 1/2 = 0.5 |
| -2 | 2-2 | 1/4 = 0.25 |
| -3 | 2-3 | 1/8 = 0.125 |
What is exponential growth in real-life?
There are many real-life examples of exponential growth. Just to mention a few, here are some applications of exponential growth.
- Population growth
- Compound interest
- Bacterial growth
Population growth
For example, suppose that the population of Florida was 16 million in 2000. Then every year after that, the population has grown by 2%. This is an example of exponential growth.
Notice that the growth rate is 2% or 0.02 and it is constant. This is important since the rate of growth cannot change.
Let us find the exponential function.
Year 2001 or 1 year after:
16,000,000 + 16,000,000 x 0.02 = 16,000,000 (1 + 0.02)
16,000,000 + 16,000,000 x 0.02 = 16,000,000(1.02)
16,000,000 + 16,000,000 x 0.02 = 16,000,000(1.02)1
Year 2002 or 2 years after:
16,000,000(1.02) + 16,000,000(1.02) x 0.02 = 16,000,000(1.02) [1 + 0.02]
16,000,000(1.02) + 16,000,000(1.02) x 0.02 = 16,000,000(1.02)(1.02)
16,000,000(1.02) + 16,000,000(1.02) x 0.02 = 16,000,000(1.02)2
Following this pattern, suppose that
- x is the number of years since 2000
- 16,000,000 is the starting amount or initial value.
- 1.02 is the rate or growth factor
Then y = 16,000,000(1.02)x
Comparing this exponential function with y = abx, we see that a = 16,000,000 and b = 1.02.
Exponential growth formula or general rule for modeling the exponential growth of a quantity
Exponential growth can be modeled with the function
y = abx for a > 0 and b >1
y = abx
x is the exponent
a is the starting amount when x = 0
b is the base, rate, or growth factor and it is a constant and it is greater than 1.
Compound interest
Savings accounts with a compounding interest rate are quite common in this day and age. Suppose you deposited $2800 in a saving account paying 4% interest rate compounded annually or once a year. How much money do you have in your saving account after 12 years?
Solution #1
Use the formula or general rule shown above to solve the problem.
y = abx
Let y be the balance after 12 years.
Let a be the principal or initial deposit. Therefore, a is equal to 2800.
Let b equal to the rate of growth.
b = 100% + 4% = 104% = 104/100 = 1.04
Let x be the number of interest periods. In this case, x is equal to 12 years.
y = 2800(1.04)x
y = 2800(1.04)12
y = 2800(1.60103221857)
y = 4482.89021
After 12 years, you will have 4482.89021 dollars in your saving account.
Solution #2
Amount of money in the saving account after 1 year
2800 + 2800 x 0.04 = 2800(1 + 0.04) = 2800(1.04) = 2800(1.04)1
Amount of amount in the saving account after 2 years
16,000,000(1.02) + 16,000,000(1.02) x 0.02 = 16,000,000(1.02) [1 + 0.02]
2800(1.04) + 2800(1.04) x 0.04 = 2800(1.04)[1 + 0.04]
2800(1.04) + 2800(1.04) x 0.04 = 2800(1.04)(1.04) = 2800(1.04)2
Following this pattern we can say the following:
The amount of amount in the saving account after 12 years is 2800(1.04)12
Bacterial growth
Suppose the population of a country is 3,000,000. A newly discovered bacteria infects 0.05% of the population each day. How many people will be infected after 15 days?
Solution
Use the formula or general rule shown above to solve the problem.
y = abx
Let y be the population after 15 days.
Let a be the population before the bacteria started infecting people. Therefore, a is equal to 3,000,000.
Let b equal to the rate of growth.
b = 100% + 0.05% = 100.05% = 100.05/100 = 1.0005
Let x be the number of days the bacteria has been infecting people. In this case, x is equal to 15 days.
y = 3000000(1.0005)x
y = 3000000(1.0005)15
y = 3000000(1.00752630696)
y = 3022578.92088
After 15 days, the population is 3022578.92088 and 3022578.92088 is closely equal to 3,022,579
Notice that the number of people infected after 15 days is equal to number of people in the population after 15 days minus the number of people in the population before the bacteria started infecting people.
3022579 - 3000000 = 22579
About 22579 people are infected with the bacteria after 15 days.