The exponential growth of coronavirus
The exponential growth of coronavirus in the world has been alarming and frightening for many.
A little bit of knowledge of algebra and the concept of exponential growth may help us understand how fast the virus will spread and how fatal it can be while doing something to keep it in check .
The information provided here is purely theoretical and educational. It is not meant to provide advice!
Teachers! Use this lesson in order to help your students appreciate a real-life application of exponential growth.
According to worldometer, we have the following important information about coronavirus.
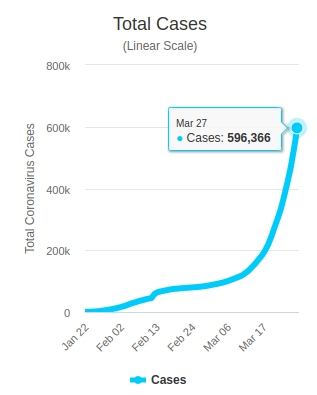
- As of March 27, 2020, about 596,000 people became infected with coronavirus.
- As of March 27, 2020, about 27000 people died of coronavirus.
- Reports of death by coronavirus started on January 22, 2020.
As already stated, our goal with this lesson is to show you how fast coronavirus can spread and how fatal this infectious disease can be while some measures are being taken to keep it in check. Therefore, we need to make some important assumptions or observations as shown below:
- Our time frame is 2 years for all computations.
- Social distancing is being practiced here and there in many parts of the world to some degree.
- Vaccines are being developed during that time frame of 2 years.
- The rate of growth and the rate of death stay about the same during our time frame of 2 years.
- The world population of 7.8 billion people is constant for about 2 years.
Modeling the exponential growth of coronavirus and the number of fatalities that may result.
Modeling the total cases or the exponential growth of coronavirus
y = abx
a is the starting amount. In this case, a is equal to the world population of 7.8 billion people as of March 27, 2020.
7.8 billion = 7,800,000,000
We need to find b.
b = 1 + ( total cases per month / world population )
Total cases per month = 596000 / 2 = 298000
b = 1 + (298000 / 7,800,000,000)
b = 1 + 0.0000382
b = 1.0000382
x is the number of months since January 22, 2020.
Our function then that models the growth of coronavirus is:
y = 7800000000(1.0000382)x
When x = 2 months, y = 7800000000(1.0000382)2
y = 7800000000(1.0000764)
y = 7,800,595,920
7,800,595,920 - 7,800,000,000 = 595,920
595920 is a good estimate since the graph shows that roughly after two months, the total cases is 596000.
Now that we know y = 7800000000(1.0000382)x is a good model for the exponential growth of coronavirus, let us see how many total cases we may have after 24 months.
When x = 24 months, y = 7800000000(1.0000382)24
y = 7800000000(1.0009172)
y = 7,807,154,160
7,807,154,160 - 7,800,000,000 = 7,154,160
In 24 months the total cases could be roughly 7,154,160
How to model the total deaths by coronavirus
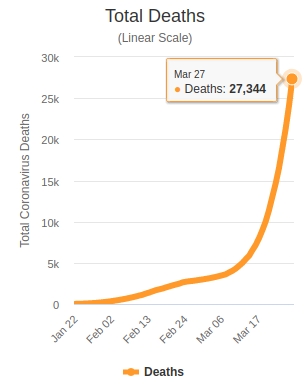The total deaths by coronavirus in the world as of March 27, 2020 according to data from the worldometers.infoy = abx
Again, a is the starting amount or the world population of 7.8 billion people as of March 27, 2020.
7.8 billion = 7,800,000,000
We need to find b.
b = 1 + ( total deaths per month / world population )
Total deaths per month = 27000 / 2 = 13500
b = 1 + (13500 / 7,800,000,000)
b = 1 + 0.00000173
b = 1.00000173
x is the number of months since January 22, 2020.
Our function then that models the total deaths is:
y = 7800000000(1.00000173)x
When x = 2 months, y = 7800000000(1.00000173)2
y = 7800000000(1.00000346)
y = 7,800,026,988
7,800,026,988 - 7,800,000,000 = 26988
26988 is a good estimate since the graph shows that roughly after two months, the total deaths is 27000.
Now that we know y = 7800000000(1.00000173)x is a good model for the total deaths by coronavirus, let us see how many total deaths we may have after 24 months.
When x = 24 months, y = 7800000000(1.00000173)24
y = 7800000000(1.00004152)
y = 7,800,323,856
7,800,323,856 - 7,800,000,000 = 323,856
In 24 months the total deaths could be roughly 323,856
If you are having problems to understand this lesson, review the lesson about modeling exponential growth.