Finding the average

Finding the average or the mean is a very straightforward concept. If you have a set of numbers, the average is found by adding all numbers in the set and dividing their sum by the total number of numbers added in the set.

We can generalize the concept of average with the formula below:

Let us illustrate with examples:

Example #1:

Get the average of the following set of numbers:

5,4,12,2,1,6

Step 1:

Find the sum of the numbers:

Sum = 5+4+12+2+1+6= 30

Step 2:

Divide 30 by 6 (the total number of numbers)

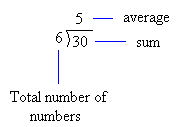
30 divided by 6 is 5, so the average or mean is 5

Example #2:

Get the average of the following set of numbers:

5,10,20,5,10

Find the sum:

Sum = 5+10+20+5+10 = 50

Divide the 50 by 5 (the total number of numbers added)

50 divided by 5 is 10, so 10 is the average or mean.

Finding the average when the numbers in the set are the same.

When all the numbers in the set are the same, it is easy to find the average. 

Example #3

Find the average of the following set of numbers:

6, 6, 6

6 + 6 + 6 = 18

18/3 = 6

Example #4

Find the average of the following set of numbers:

12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12 

12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 132

132/11 = 12

What can we conclude from example #3 and example #4?

Finding the average when some of the numbers in the set are negative numbers.

Example #5

-5, 2, -1, 8

-5 + 2 + -1 + 8 = 4

4/4 = 1

Example #6

-8, 2, -11, 3, 0, 2

-8 + 2 + -11 + 3 + 0 + 2 = -12

-12/6 = -2

Example #7:

Mr. Peter collected 125 pencils from students during the past 5 days. On the average, how many pencils did he collect each day?

Average = 125/5 = 25

Example #8:

Last week, Samuel ordered pizza every day. After collecting all his receipts and getting the total, he realized that he spent a total of 63 dollars on pizza. On the average, how much money did he spend on pizza each day?

Average = 63/7 = 9

Other ways to find the average of a data set

There are many other ways to find the average of a data set. The most common ways to find the average is to look for either the mean (described in this lesson), the mode (the most frequently occurring number or numbers), and the median (the value in the middle).

The weighted average is used by teachers a lot to calculate your final grade or to calculate the average price of a share.

For example, suppose you buy 20 shares of a company and each share costs you 5 dollars. Five years later, you buy 10 more shares and each share costs 50 dollars this time.

You must use a weighted mean to find the average price of a share.

Average price of a share = Total cost / number of shares

Average price of a share =  (20 × 5 + 10 × 50) / (20 + 10) = 600 / 30 = 20 dollars.

As you may have noticed so far, the average formula used to find the average is not always the same. The lesson about types of averages will help you become familiar with 8 types of averages and the formula that you should use for each type.