Types of Polygons
There are many different types of polygons. To explore them all along with their properties can be a course in itself. Basically, a polygon is a closed plane figure made of three or more sides.
Examples of Polygons
Triangle
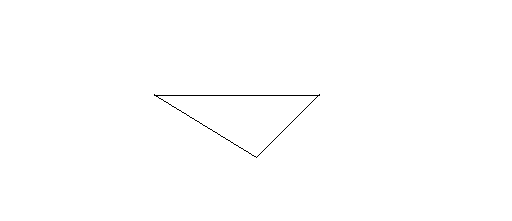
A triangle has the following basic properties:
- 3 sides and 3 vertices
- No diagonal
- Sum of the interior angles is 180 degrees
Quadrilateral
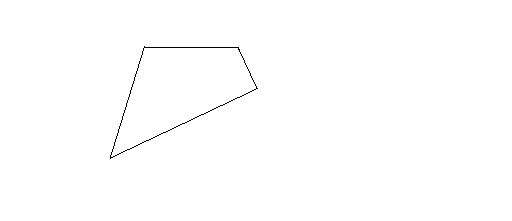
A quadrilateral has the following basic properties:
- Four sides and four vertices
- Two diagonals
- Sum of the interior angles is 360 degrees
Pentagon
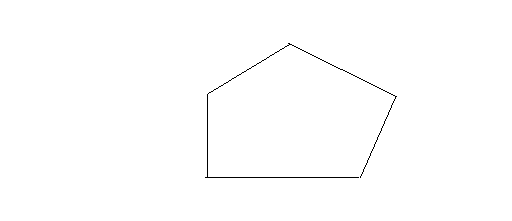
A pentagon has the following basic properties:
- Five sides and five vertices
- Five diagonals
- Sum of the interior angles is 540 degrees
Hexagon
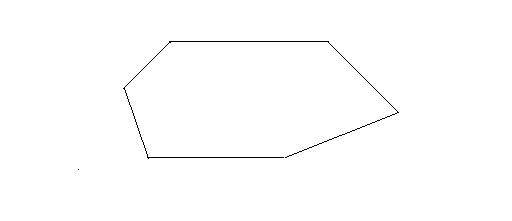
A hexagon has the following basic properties:
- Six sides and six vertices
- Nine diagonals
- Sum of the interior angles is 720 degrees
Heptagon
A heptagon has the following basic properties:
- Seven sides and seven vertices
- Fourteen diagonals
- Sum of the interior angles is 900 degrees
Octagon
An octagon has the following basic properties:
- Eight sides and eight vertices
- Twenty diagonals
- Sum of the interior angles is 1080 degrees
Nonagon
A nonagon has the following basic properties:
- Nine sides and nine vertices
- Twenty-seven diagonals
- Sum of the interior angles is 1260 degrees
Decagon
A decagon has the following basic properties:
- Ten sides and ten vertices
- Thirty-five diagonals
- Sum of the interior angles is 1440 degrees
Dodecagon
A dodecagon has the following basic properties:
- Twelve sides and twelve vertices
- Fifty-four diagonals
- Sum of the interior angles is 1800 degrees
Types of Polygons Based on their Sides and Angles
If we classify polygons based on their sides and angles, then the polygons are either regular polygons or irregular polygons.
Regular Polygons
If a polygon is a regular polygon, all sides are the same and all interior angles are the same. See below some examples of regular polygons. Starting from left to right and from top to bottom, the regular polygons shown below are the triangle, the square, the regular pentagon, the regular hexagon, the regular heptagon, the regular octagon, the regular nonagon, and the regular decagon.
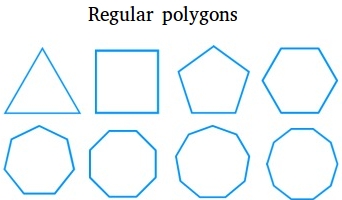
A square is a regular polygon because the sides are equal and each of the four interior angles is equal to 90 degrees.
Irregular Polygons
If a polygon is an irregular polygon, the sides are not the same and the interior angles are not the same. See below some examples of irregular polygons.
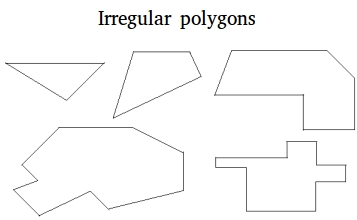
For example, a rectangle is an irregular polygon because only opposite sides are equal although each of the four interior angles is equal to 90 degrees.
Types of Polygons Based on their Angles
Polygons can be classified based on the size of the interior angle made by adjacent sides.
If there is an interior angle that is bigger than 180 degrees, the polygon is a concave polygon.
If no interior angle is bigger than 180 degrees, the polygon is a convex polygon.
See the lessons about convex polygons and concave polygons to learn more.
If you can build a polygon so that all interior angles are equal, then the polygon is an equiangular polygon. Notice that the sides of the polygons may not be the same. A rectangle is an equiangular polygon.
A triangle can be further classified into many different types such as scalene triangle, equilateral triangle, isosceles triangle, etc...
See the lesson about types of triangles to learn more
A quadrilateral can be further classified into many different types such as rectangle, parallelogram, rhombus, trapezoid, etc...
See the lesson about types of quadrilaterals to learn more
Polygons are all around. Take a close look around you in your house, at the work place, or in an amusement park, you will find many real life examples of polygons.